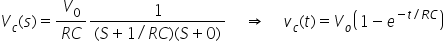Laplace Transform 

Laplace transforms and their inverse are a mathematical technique which allows us to solve differential equations, by primarily using algebraic methods. This simplification in the solving of equations, coupled with the ability to directly implement electrical components in their transformed form, makes the use of Laplace transforms widespread in both electrical engineering and control systems engineering.

This note is a recap/review of Laplace theory and reference which can be used while carrying out day to day work.  It is not an introduction or tutorial and does assume some prior knowledge of the subject.

Theory

The Laplace transform, named after Pierre-Simon Laplace who introduced the idea is defined as:

 $$F(s)=L\left\{f(t)\right\}={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-st}}f(t)dt$$

where: S = σ + iω,  (σ and ω as real numbers)

the result is a function of s, and the transform can be written as:

 $$F(s)=L\left\{f(t)\right\}$$

Give the transform, the inverse can be found from:

 $$f(t)=L^{-1}\left\{F(s)\right\}=\frac{1}{2\pi i}\underset{T\to 0}{\lim }{\displaystyle \underset{\gamma -iT}{\overset{\gamma +iT}{\int }}{e}^{st}}F(s)ds$$

While we can use the above equations to find the Laplace transform (or it's inverse) for a given function, in practice the use of table is more common.  The following table lists the more common transforms and their inverse:

Time Function f(t)	Laplace Transform F(s)
, unit impulse	1
, unit step
where

Useful Operations

Linearity
Multiplication (by constant)
Real Shift Theorem
Complex Shift Theorem
Scaling
Derivative (1st)
Derivative (nth)
Integral
Convolution
Heaviside (step) Function

Partial Fractions

In finding the inverse transforms, it is helpful if the equation to be solved is expressed as a sum of fractions.  Partial fractions are a way to achieve this and the process is called resolving partial fractions. 

To be able resolve partial fractions, the numerator needs to be of lesser degree than the denominator and depending on the type of partial fraction:

Linear factors in the denominator:

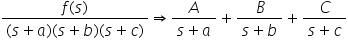
Repeated linear factors in the denominator:

 

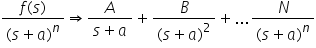
Quadratic factors in the denominator:

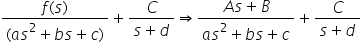
Example: the following example illustrates how to use the method of partial fractions to resolve a simple equation using linear factors. Ffind the partial fractions of:

 

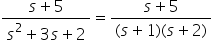
which can be resolved into

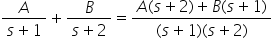
From the above, it can be seen that: 

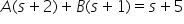
By choosing values of s to make A or B equal to zero (s = -2, s = –1), the above can be solved to give A (=4) and B (=-3), giving us the final solution:

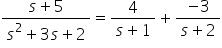
Application

One of the great things about Laplace Transforms is that the core electrical quantities (resistance, inductance and capacitance) can be easily represented in their Laplace form; simplifying the solving of circuits.  The table below summaries the time and Laplace representation of each quantity:

		Time domain		Laplace domain
		v(t)	i(t)	F(s)	V(S)	I(S)
Resistor	R
Inductor	L	$$L=\frac{di(t)}{dt}$$
Capacitor	C

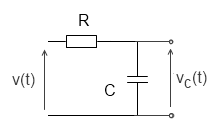Example:  consider a series circuit consisting of a resistor and capacitor as shown. A step voltage v(t) equal to V₀ is applied at time zero.  What is the form of the voltage across the capacitor, v_c(t).

To represent the input voltage, we can use the Heaviside (step):

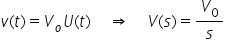
From the above table, the Laplace transform of the current, i through the circuit can be written directly as:

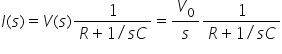
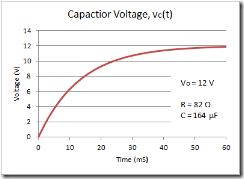
and the Laplace voltage across capacitor as:

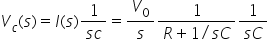
Rearranging the equation and taking the inverse Laplace transforms, gives: