Fault Calculation - Symmetrical Components
| Symbol |
- |
Definition |
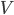 |
- |
system voltage
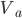 , , 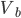 , , 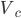 - unbalanced voltages - unbalanced voltages
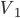 , , 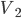 , , 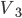 - symmetrical voltages - symmetrical voltages |
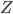 |
- |
circuit impedance
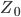 - earth fault impedance - earth fault impedance
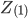 - positive sequence impedance - positive sequence impedance
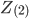 - negative sequence impedance - negative sequence impedance
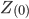 - zero sequence impedance - zero sequence impedance |
For unbalanced conditions, the calculation of fault currents is more complex. One method of dealing with this is symmetrical components. Using symmetrical components, the unbalanced system is broken down into three separate symmetrical systems:
- Positive sequence – where the three fields rotate clockwise
- Negative sequence – where the three fields rotate anti-clockwise
- Zero sequence – a single field which does not rotate
The positive sequence network rotates clockwise, with a phase of 120° between phases as per any standard a.c. system.
The negative sequence network rotates anti-clockwise, and the zero sequence network with each phase together (0° apart).
_thumb.png)
Basic Symmetrical Component Theory
Mathematically, the relationship between the symmetrical networks and the actual electrical systems, make use of a rotational operator, denoted by a and given formally by:
_thumb.png)
Perhaps more simply, the a operator can be looked at as a 120° shift operator. It can also be shown that the following conditions hold true:
_thumb.png)
By using the a operator, any unbalanced any unbalance three-phase system Va, Vb, Vc can be broken down into three balanced (positive, negative and zero sequence) networks V1, V2, V0.
| Unbalanced Network |
|
Symmetrical Network |
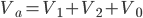 |
|
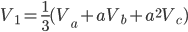 |
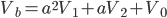 |
|
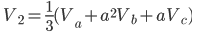 |
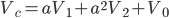 |
|
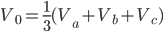 |
The operator a, is the unit 120° vector: a = 1|120°. Note: a3=1 and a-1 = a2
Fault Solutions
Once the sequence networks are known, the determination of the magnitude of the fault is relatively straightforward.
The a.c. system is broken down into it's symmetrical components as shown above. Each symmetrical system is then individually solved and the final solution obtained by superposition of these (as shown above).
For the more common fault conditions, once the sequence networks are known, we can jump directly to the fault current. During a fault and letting Un, be the nominal voltage across the branch, the use of symmetrical components gives the following solutions (excluding fault impedance):
| Type of Fault |
Initial Fault Current |
Comments |
| three phase |
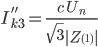 |
|
| phase to phase |
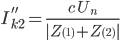 |
|
| phase to phase |
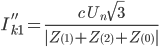 |
|
| phase to phase to earth |
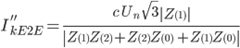
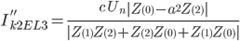
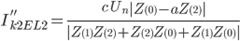 |
Note: the example given assumes a phase to phase fault between L2 and L3 (then shorted to earth) |
Sequence Impedance Data
Positive, negative and zero sequence impedance data is often available from manufacturers.
A common assumption is that for non-rotating equipment the negative sequence values are taken to be the same as the positive.
Zero sequence impedance values are closely tied to the type of earthing arrangements and do vary with equipment type. While it is always better to use actual data, if it is not available (or at preliminary stages), the following approximations can be used:
| Element |
Z(0) |
| Transformer |
|
| No neutral connection |
∞ (infinity) |
| Yyn or Zyn |
10 to 15 x X(1) |
| Dyn or YNyn |
X(1) |
| Dzn or Yzn |
0.1 to 0.2 x X(1) |
| Rotating Machine |
|
| Synchronous |
0.5 x Z(1) |
| Asynchronous |
zero |
| Transmission Line |
3 x Z(1) |
Approximate Zero Sequence Data (source: Schneider)
Related Notes