Induction Motor Equivalent Circuit
Induction motors are frequently used in both industrial and domestic applications. Within the induction motor, an electrical current in the rotor is induced by a varying magnetic field in the stator winding. The rotor current produces it's own magnetic field, which then interacts with the stator field to produce torque and rotation.
Induction Motor Concepts
One way to analyse and understand the operation of an induction motor is by the use of an equivalent circuit. Before jumping into the equivalent circuit, a few concepts are useful.
Slip
Induction motors are asynchronous. The stator magnetic field rotates at the motors synchronous speed (ns). The rotor can never rotate at synchronous speed, otherwise there would be no induced current. Typically the rotor full speed will between 2 and 6% that of the synchronous speed. The difference between the motors synchronous and actual asynchronous speed is known as the slip
The difference between the motors synchronous speed (ns) and actual rotor speed (nr) is known as the slip (s). Slip can be expressed as either a fraction or percentage:
_thumb.png)
Frequency
From magnetic winding theory, the relationship between frequency in the stator (f), number of pole pairs (p) and the synchronous speed is given by:
_thumb.png)
Within the rotor, the frequency (fr) is given by the speed difference between that of the rotor and stator:
_thumb.png)
which when combined with the above equation for slip, gives:
_thumb.png)
the synchronous speed in revolutions per second is:
_thumb.png)
and in revolutions per minute (rpm)
_thumb.png)
The quantity ns is the speed at which the flux rotates relative to the stator and sns the speed of the rotor flux relative to the rotor. However, the rotor itself is rotating at nr, giving a total rotor flux speed of:
_thumb.png)
The rotational speed of the stator flux and rotor flux are identical. This is the same as in a transformer and allows us to model the behaviour of an induction as a transformer with an air gap.
Induction Motor Equivalent Circuit
From the preceding, we can utilise the equivalent circuit of a transformer to model an induction motor.
_thumb.png)
In the equivalent circuit R1 represents, the resistance of the stator winding and X1 the stator leakage reactance (flux that does not link with the air gap and rotor). Magnetising reactance required to cross the air gap is represented by Xm and core losses (hysteresis and eddy current) by Rc.
An ideal transformer of N1 and N2 turns respectively represents the air gap. For the rotor side, the induced emf is affected by the slip (as the rotor gains speed, slip reduces and less emf is induced). The rotor resistance and reactance are represented by R2 and X2; with X2 being dependant on the frequency of the inductor rotor emfs.
The rotor circuit, the current I2 is given by:
_thumb.png)
which can be rewritten as:
_thumb.png)
The above equality allows the equivalent circuit to be drawn as:
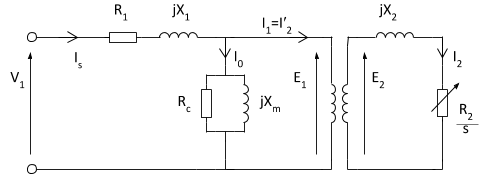
Simplified Equivalent Circuit
The equivalent circuit shown above has removed the dependence on slip for determining the secondary voltage and frequency. Consequently the circuit can be simplified by eliminating the ideal transformer and referring the rotor's resistance and reactance to the primary (denoted by ′).
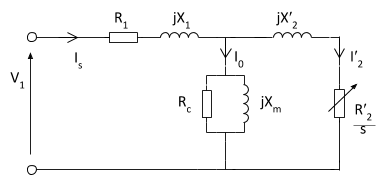
The referred values are calculated by multiplying them by k2, where k is the effective stator/rotor turns ratio.
Note: it is relatively straightforward to obtain the equivalent circuit parameters by testing. Typically this would involve a d.c. test, no-load test and locked rotor test.
Calculation of Motor Performance
The simplified equivalent circuit allows us to calculate the operating parameters for an induction motor.
Note: calculations are vector quantities. Should complex representation be used, then phase shift, power factors, etc. automatically fall out of the calculations.
Motor Current
Once the equivalent circuit parameters are known, it is easy to calculate the motor current, by reducing the circuit to an equivalent impedance Zeq, giving:
_thumb.png)
By inspecting the equivalent circuit, we can see that Zeq is of the form:
_thumb.png)
From this equation, it can be seen that as the rotor speeds up (slip reduces), the circuit impedance increases and stator current decreases.
Note: if you need more help on how to reduce the equivalent circuit to a single impedance, you can have a look at our Network Theory – Introduction and Review note.
Motor Power
As a simplification, if we neglect the core losses (Rc and giving Is = I′2) the power (Pin) delivered to the motor per phase is given by:
_thumb.png)
The power loss dissipated by the windings is given by:
_thumb.png)
The difference between the power supplied to the motor and losses in the windings is the power (Pm) delivered to the connected load. This (per phase) is given by:
_thumb.png)
and for all three phases
_thumb.png)
Motor Torque
Knowing that power can be the motor torque (M) multiplied by the angular velocity (ω), this can be rearranged and a formulae for torque (T) derived:
_thumb.png)
and
_thumb.png)
which combined with the power equation gives
_thumb.png)
Power Equivalent Diagram
The above illustrates how to calculate various motor parameters by utilising the simplified equivalent circuit and neglecting core iron losses. For more accurate calculations, the core iron losses can be included. From the above, it is easily possible to visualise the full motor power flow:
- power input to the stator (Pin)
- → Stator Winding Losses
- → Core Iron Losses
- → Rotor Winding Losses
- → Power to Load (Pm)
- → Windage & Friction Losses
Windage and power losses are necessary to give the full picture of how the input power is to a motor is translated to shaft output power.
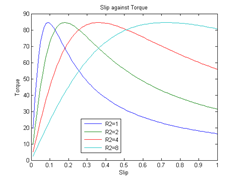
Torque and Slip - Example
To see how the equivalent circuit can be used, we can look at an example of investigating torque-slip characteristics.
To simplify the analysis, we ignore the magnetising current and iron losses (i.e. Rc=jXm=0). From the simplified equivalent circuit the magnitude of the stator current Is is given by:
_thumb.png)
and substituting into the torque equation gives:
_thumb.png)
Matlab Script
The torque-slip plot was produced with Matlab using the following script:
V1 = 400/sqrt(3); % phase voltage (V)
R1 = 1; % stator winding resistance (?)
X1 = 3; % stator reactance (?)
X2 = 8; % rotor reactance (?)
p=4; % number of pole pairs
f=50; % frequency, Hz
ns=60*f/p; % synchronouse seed (rev.s-1)
s = 0:0.01:1; % slip values
torque=[]; curve={};
for R2 = [1 2 4 8] % rotor winding resistance
k = ((90*R2*V1^2)./(pi*ns*s));
d = (R1+R2./s).^2+(X1+X2)^2;
torque(:,end+1) = k./d;
curve{end+1} = strcat(' R2=', num2str(R2));
end
plot(s,torque);title('Slip against Torque');
xlabel('Slip'); ylabel('Torque'); legend(curve,0)
Example - consider a three phase motor 400 V motor with 4 pole pairs and the following equivalent circuit parameters R1=1 Ω, X1=3 Ω, R′2=1 Ω and X′2=2 Ω. Plot the torque slip characteristic. Also consider the effect of varying the referred rotor resistance, R′2 (1, 2, 4 and 8Ω).
Symbols
f - frequency (stator circuit), Hz
fr - frequency (rotor circuit), Hz
I1, Is - stator current, A
I2 - rotor current, A
k - effective turns ratio of the stator/rotor circuits
N1 - equivalent circuit ideal transformer primary turns
N2 - equivalent circuit ideal transformer secondary turns
nr - rotor speed, rev.s-1 or rpm
ns - synchronous speed, rev.s-1 or rpm
p - number of pole pairs (2 poles = 1 pole pair)
Pc - motor iron (core) losses, W
Pin - motor input power, W
Pm - power delivered to the load, W
Pw - motor winding (stator + rotor) power loss, W
R1 - rotor circuit resistance,Ω
R2 - stator circuit resistance, Ω
s - slip
T - motor torque, N.m
ω - angular velocity of rotor, rad.s-1
X1 - stator leakage reactance, Ω
X2 - rotor circuit reactance, Ω
Xm - magneising reactance, Ω