Power Transformers - An Introduction
One of the fundamental requirements of an alternating current distribution systems it to have the ability to change the magnitude of voltages. It is more efficient to transmit power at high voltages over long distances, whereas it is safer and more practical to use a low voltage to drive appliances and equipment. Transformers are used to achieve this.
General Theory
A transformer is a device consisting of two (or more) windings coupled together magnetically. A changing current in one winding (normally called the primary), will generate a magnetic field. This magnetic field links with the second winding (normally called the secondary) and will induce a current into this winding.
_thumb.png)
Transformer operation principal
The illustration shows how a voltage V1 applied to the primary winding of N1 turns, creates a current I1 which causes the generation of the magnetic flux in the core. The flux in the core with generates voltage V2 in the secondary winding of N2 turns, giving a current I2 in the load.
Core - to facilitate distribution of the magnet field, transformer cores are usually made of steel laminations. Laminations are preferable to a solid steel cores as they reduce losses.
The relationship between voltage, number of turns and current is given by:
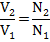 and
and 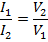
Tip - transformer efficiencies are high and by assuming the input power equals the output power the above voltage and current relationships are easily derived: input power (in VA) = V1 x I1 with equals the output power = V2 x I2, which rearranged give the above.
Transformers are not perfect and there are losses. This can be divided into two types:
- I2R losses - in the windings occur due to resistive losses in both the primary and secondary windings. Resistive losses increase with load magnitude.
- Core losses - result from eddy current and hysteresis losses in within the transformer core. Losses in the core are fairly constant regardless of loading.
The total loss is the sum of the core losses Pc and the resistive losses due to primary current I1, primary winding resistance R1, secondary current I2 and secondary winding resistance R2:
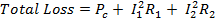
The efficiency of the transformer can be expressed as:
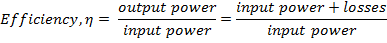
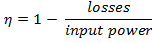
Three Phase Transformers
_thumb.png)
Transformer operation principal Three phase transformers can be made by combining single phase transformers. One of the more common implementations is to construct a core of three limbs closed at the top and bottom. Each individual cores contains the primary and secondary winding of a single phase.
Windings may be connected either in star or delta depending on requirements. The image shows one start connected and one delta connected winding.
Practical Aspects
Vector Group
Transformers can be wound in various configurations (delta-star, star-star, etc.). Depending on the configuration there will be a phase shift between the primary and secondary of the transformer. The transformer configuration and phase shift is termed the vector group.
The vector group is represented by a capital letter for the primary winding, a lower case letter for the secondary winding and followed by a number (1 to 11). The letter indicated the winding arrangement - D=Delta, Y=Star and Z=Zigzag. The number is the phase shift in multiples of 30 degrees. For example:
Dy11 - delta connected primary, star secondary, 330° (-30°) phase shift
Dd0 - delta connected primary, delta secondary, no phase lag
Sometimes a third letter is added to indicated the neutral is brought out, for example Dyn11 (delta-star transformer with the secondary neutral brought out).
Transformer Tapping

Three phase transformer (core type winding) The nominal voltage of a transformer is related to the turns ration between the primary and secondary. In use the primary voltage can vary and the secondary current can vary. Both these will affect the output voltage of the transformer.
To cater for varying primary and secondary conditions, transformers are often fitted with taps on one of the windings; so that the turns ratio can be adjusted somewhat. These are often expressed as numbers.
For example, a low voltage transformer may have -5%, -2.5%, 0%, +2.5% and +5% taps. At 0% tap the transformer will be operating at its designed turns. At +2.5% the transformer secondary voltage will be 2.5% larger than what it would be if set at 0% (for the same primary voltage and secondary current).
An example of use would be setting a +2.5% or +5% tap on a transformer which is heavily loaded to help compensate for the voltage drop in the cables.
Temperature Derating
According to the standards[1][ 2][3], transformers are designed for:
- a maximum temperature - 40 °C
- 30 °C monthly average of the hottest month
- 20 °C yearly average
- outdoor transformer minimum temperature -25 °C
- indoor transformer minimum temperature -5 °C
When the transformer is designed for service where the temperature of the cooling air exceeds the maximum allowable, the temperature rise limits shall be reduced by the amount of the excess.
Alternatively the temperature differences can be taken into account by adjusting the transformer capacity:
Ambient temperature
(annual average)
|
Capacity |
|
-20 °C
|
124%
|
|
-10 °C
|
118%
|
|
0 °C
|
112%
|
|
+10 °C
|
106%
|
|
+20 °C
|
100%
|
|
+30 °C
|
93%
|
Altitude Derating
Transformers are designed for an altitude of 100 m above sea level. For other altitudes, the limit of the average winding temperature rise shall be reduced by[2][3]:
- oil immersed, air naturally cooled - 1 K for every 400 m above design altitude
- oil immersed force cooled - 1 K for every 200 m above design altitude
- oil immersed water cooled - no correction for altitude
- dry-type air naturally cooled - 2.5% for every 500 m above design altitude
- dry-type air force cooled - 5% for every 500 m above design altitude
References
- [1] - IEC 60076-1: 'Power transformers - General', 2000-2004
- [2] - IEC 60076-2: 'Power transformers - Temperature rise', 1997
- [3] - IEC 60076-11; 'Power transformers - Dry-type transformers
- [4] - Siemens: ‘Application Manual - Part 2: Draft Planning', 2007