The ac resistance of conductors
In a previous article I looked at the
dc resistance of conductors and in this article we turn our attention to ac resistance. If you have not read the previous article, now may be a good time to do so. The ac resistance of a conductor is always larger than the dc resistance. The primary reasons for this are 'skin effect' and 'proximity effect', both of which are discussed in more detail below.
In a previous article I looked at the dc resistance of conductors and in this article we turn our attention to ac resistance. If you have not read the previous article, now may be a good time to do so.
The ac resistance of a conductor is always larger than the dc resistance. The primary reasons for this are 'skin effect' and 'proximity effect', both of which are discussed in more detail below.
There are various methods to take into account these effects, but I'll concentrate on those given in IEC 60287 (Electrical cables - calculation of the current rating). In addition to being widely accepted, the method is also part of a standard which gives it some legitimacy.
The standard take skin and proximity effects into account with the following formulae:
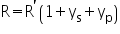
Where:
R = the ac resistance of the conductor
R' = the dc resistance of the conductor
ys = a skin effect factor
yp = a proximity effect factor
While the above formulae is pretty straight forward, working out the skin and proximity effect factors is a little more involved, but still not too difficult.
Skin Effect
As the frequency of current increases, the flow of electricity tends to become more concentrated around the outside of a conductor. At very high frequencies, often hollow conductors are used primarily for this reason. At power frequencies (typically 50 or 60 Hz), while less pronounced the change in resistance due to skin effect is still noticeable.
The skin effect factor ys is given by:
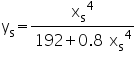
where:
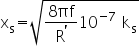
f = supply frequency in Hertz
ks = skin effect coefficient from the table below
Proximity Effect
Proximity effect is associated with the magnetic fields of conductors which are close together. The distribution of the magnetic field is not even, but depends on the physical arrangement of the conductors. With the flux cutting the conductors not being even, this forces the current distribution throughout the conduit to be uneven and alters the resistance.
The formulae for the proximity effect factor differs dependant on wether we are talking about two or three cores.
- two core cables or two single core cables
- for three core cables or three single core cables
Where (for both cases):
dc = diameter of the conductor (mm)
s = distance between conductor axis (mm)
kp = proximity effect coefficient from the table below
Note:
1. for three single core with uneven spacing s = √(s1 x s2)
2. for shaped conductors, yp is two thirds the value calculated above, with
dc = dx = diameter of equivalent circular conductor of same cross sectional area (mm)
s = (dx + t), where t is the thickness of insulation between conductors (mm)
Coefficients ks and kp
| | ks | kp |
| Copper | Round stranded or solid | 1 | 1 |
| Round segmental | 0.435 | 0.37 |
| Sector-shaped | 1 | 1 |
| Aluminium | Round stranded or solid | 1 | 1 |
| Round 4 segment | 0.28 | 0.37 |
| Round 5 segment | 0.19 | 0.37 |
| Round 6 segment | 0.12 | 0.37 |
Summary
Should you need to calculate the resistance of a conductor, I hope this article (and the accompanying dc article) can help. In summary the procedure is fairly straight forward:
- Look up the dc resistance at 20 0C from the IEC 60287 table, see first article
- Adjust for operating temperature as show in the first article
- Adjust for skin and proximity effects as shown in this article
If anyone has any comments or anything to add, please do so below.
<- The dc resistance of conductors