Cable Sheath and Armour Loss
When sizing cables, the heat generated by losses within any sheath or armour need to be evaluated. When significant, it becomes a factor to be considered in the sizing of cables. To understand how sheath and armour losses affect the sizing of cables, you can review the post: IEC 60287 Current Capacity of Cables - Rated Current.
This note looks at how to obtain the necessary loss factors for use within the IEC 60287 calculation. In addition, the loss factors quantify the ratio of losses in the sheath to total losses in all conductors and have application outside the IEC 60287 standard.
Calculation of Sheath and Armour Loss
Any cable sheath (or screen) the loss λ1, consists of two components:
- λ1' - losses caused by circulating currents. These losses only occur in single core cables and for any circulating current to be present, it is necessary to the sheaths of each cable to be bonded at two or more points along its length.
- λ1'' - losses caused by eddy currents. These are small circulating currents setup in the sheath due to changing magnetic fields.
The loss in armour is considered as only one component, λ2.
Sheath and armour losses are only applicable to alternating current (a.c.) cables. The actual formula for calculation of sheath and armour loss depend on the installation and arrangement of cables. The tables below presents some of the common installation situations and are based on equations given in IEC 60287:
Calculation of sheath or screen loss in - Single Core Cables
For installations bonded only at one point, circulating currents are not possible and the loss is zero. Except in the case of large segmental type conductors (see Some Special Cases below), eddy current loss λ1'', for single core cables can be ignored.
| | Sheath Circulating Current Loss, λ1' |
Single core cables
- trefoil, bonded at both ends | |
Single core cables
- flat, with transposition, bonded at both ends
| |
Single core cables
- flat, without transposition, bonded at both ends | λ11′ - loss factor for the outer cable with the greater losses
λ12′ - loss factor for the outer cable with the least losses
λ1m′ - loss factor for the middle cable
where:
|
Calculation of sheath or screen loss in - Multi-Core Cables
Due to any sheath or screen surrounding all cores, the possibility of circulating current does not exist, and the λ1' loss can be ignored. Eddy current loss, λ1'' does need to be considered.
| | Sheath Eddy Current Loss, λ1'' |
| Two core cable - common sheath, unarmoured | - for round or oval conductors
- for sector shaped conductors
|
| Three core cable - common sheath, unarmoured | - round or oval conductors, Rs ≤ 100 µΩ.m-1
- round or oval conductors, Rs >100 µΩ.m-1
- for sector shaped conductors (any Rs)
|
| Two or three core cable - steel tape armour | Multiple the unarmoured cable factor by:
|
Cables with each core in a separate sheath or pipe type cables
|
where:
|
Calculation of armour loss
For armoured cables, the losses are estimated as shown.
| | Armour Loss, λ2 |
| Non-magnetic armour | Use equation for λ1'', substituting: - parallel combination of sheath and armour resistance for Rs
- root mean square of sheath and armour diameter for d
|
Single core cables - steel wire armour
| General advice is not to use magnetic armour for single core cables.
If required, then the guidelines given in IEC 60287 on estimating losses should be followed. |
| Two core cable - steel wire armour | |
| Three core cable - steel wire armour | - round conductor
- sector shaped conductor
|
Calculating the Parameters
Sheath (Rs) or armour (RA) resistance - values used above are calculated at their operating temperature. The operating temperature (in °C) and resistance can be determined from:
- for any sheath
- for any armour
- for the cable sheath
- for the cable armour
Note: for calculation of the dielectric loss Wd, refer to our Dielectric loss in cables note.
Cable Reactance - for single core cables, where there is significant spacing between conductors, it is necessary to use the reactance in the calculating of circulating current loss. Accurate values for reactance can be obtained from cable manufacturers or by using software. Alternatively, the following equations can be used to estimate the reactance (Ω.m-1):
Single core cable reactance estimates (assume bonded at both ends)
- trefoil or flat without transposition
- flat with transposition
- mutual reactance of flat formation cables
Steel tape armour resistance - depending on how steel tape is wound, the resistance can be estimated as follows:
- tapes laid longitudinally - calculate the resistance as that of an equivalent cylinder (same mass and diameter)
- tapes laid ≈54° to cable axis - use twice the value obtained from (1)
- tapes with a very short lay - take resistance as infinite (neglect losses)
- tapes with a very short lay (double layered) - use twice the value obtained form (1)
Cable Transposition
Transposing of cables (see image) is a technique to reduce the circulating currents within cable sheaths and consequently increase the rating of the cable.
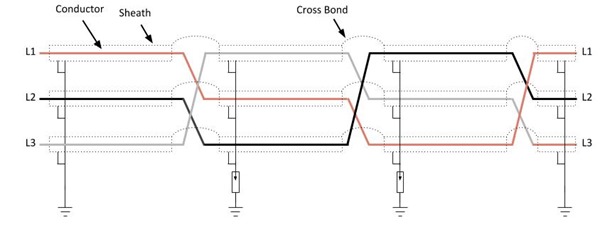 Transposed and cross bonded cable
Transposed and cross bonded cable By cross bonding the sheath the induced currents are in opposite directions, cancelling each other out and significantly improving the current rating of the cable. Transposing the cables ensures that the reactance balance out and aids in implementation.
At intermediate transposition points, over voltage devices are installed to protect the cable and personnel in the event of voltage build up during faults.
In practice, three minor sections (part between the cross bond) would from a major section (three full transpositions). It makes sense to do these at each joint point - at each cable drum length.
Transposition and cross bonding are normally carried out in link boxes.
Some Special Situations
Large segmental type conductors
Eddy current losses λ1'', are normally small relative to other losses and can be ignored for single core cables. This changes for large conductors, which are of a segmented construction. Under these conditions, the eddy current loss should be considered.
For this condition, the value of λ1'' is derived from the circulating current loss factor λ1' by:
where:
- for cables in trefoil
- for cable in flat formation
Single core cables - variation of route spacing
If the spacing if not maintained the same for the full cable route than the reactance will vary along the route. In instances such as these, an equivalent overall reactance can be calculated from:
- where la, lb, ... are the section lengths and Xa, Xb, ... are the reactance of each section
Symbols
| A | - armour cross sectional area, mm2 | | R | - conductor a.c. resistance, Ω.m-1 | | RA | - armour resistance maximum at operating temperature, Ω.m-1 | | RA20 | - armour resistance at 20 °C, Ω.m-1 | | Rs | - sheath or screen resistance at maximum operating temperature, Ω.m-1 | | Rs20 | - sheath or screen resistance at 20 °C, Ω.m-1 | | X | - sheath or screen reactance, Ω.m-1 | | Xm | - mutual reactance (sheath one cable to conductors of other cables), Ω.m-1 |
| λ1 | - ratio of sheath loss to total conductor loss | | λ2 | - ratio of armour loss to total conductor loss |
| λ1' | - sheath loss caused by circulating currents | | λ1'' | - sheath loss caused by eddy currents | | | c | - distance between axis of conductors, mm | | d | - mean diameter of sheath or screen, mm | | dA | - mean diameter of armour, mm | | r1 | - circumscribing radius of sector shaped conductors, mm | | s | - axial separation of conductors, mm | | t | - insulation thickness between conductors, mm | | T1 | - thermal resistance between conductor and sheath, K.m.W-1 | | T2 | - thermal resistance between sheath and armour, K.m.W-1 |
| θ | - maximum conductor temperature, °C | | θar | - maximum operating temperature of armour, °C | | θsc | - maximum operating temperature of screen, °C | | ω | - angular frequency (2πf) | | µ | - relative magnetic permeability of armour | | δ | - equivalent thickness of armour, mm | |
See Also