RLC Circuit, Resistor Power Loss - some Modelica experiments

Modelica is an open source (free) software language for modelling complex systems. Having never used it before, I thought I would download a development platform and see how it stacked up. This is where I spent my Saturday.
Modelica is a software language aimed at solving algebraic and ordinary differential equations. As such, it can be used for a wide variety of electrical simulation problems. The language is extensive and does entails a learning curve. Evaluation for only one day probably does not do it justice (or given that I like the language, it may do justice). Even with the limited time I played with the software, I was able to model and gain a better insight to a particular problem which has been at the back of my mind for some time.
Modelica
To find out more about Modelica you can visit the projects site at: www.modelica.org. With being a language specification, you can run Modelica on different platforms. The main site lists many of these (some commercial and some free). For the examples in this note, I used the free software tool, OpenModelica which you can download from www.openmodelica.org.
As an object orientated language, Modelica lets you play with different systems (electrical, mechanical, hydraulic, etc.) and use these together to build complex representations of real world systems. The implementation platforms allow you to build your model as text based classes or as a diagram by visually connecting function blocks.
RLC Circuit - Power Loss across the resistor
Rather than look as something I already know the answer for, I decided to test Modelica by looking at the energy lost in the resistor of an RLC circuit during charging from a pulsed d.c. supply.
Recently I wrote a couple of notes on capacitor charging and energy storage applications. In these posts, I looked at how much energy is lost across any resistance if a capacitor is charged from a constant d.c. source. As it turns out, as much energy is lost across the resistor as is stored in the capacitor. Not the most efficient way to store energy. If your interested in delving into this theory, you can check out:
Knowing that we lose half the energy across a resistor when charging from a steady d.c. supply; my interest revolves around seeing if this is also true for a pulsed d.c. supply. Does the energy loss slowly build up to equal that stored or do we lose less energy? This is the problem I set myself as the test case.
While deriving state space equations and modelling these directly in Modelica is a valid approach (see later in the note), I decided to first use the pre-built electrical blocks in a process flow type of approach. To me this is the way I would envisage using Modelica to solve real problems; only resorting to deriving my own models in special circumstances.
Process Flow Diagram Approach
The OpenModelica editor lets you drag and drop the blocks, connect them up and run your simulation. The following image shows the model I put together.
![Image [3] Image [3]](http://myelectrical.com/Portals/0/SunBlogNuke/2/WindowsLiveWriter/RLCPowerLossAcrossaResistorsomeModelicae_7D48/Image%20%5B3%5D_thumb.png) Modelica RLC Circuit Model - Block Diagram Approach
Modelica RLC Circuit Model - Block Diagram Approach
For the voltage source, I used a constant d.c. source and switched it via an ideal switch to form the pulses. While developing the model, I did experiment with the d.c. pulsed voltage source, but it didn't work well for me. When the output voltage was turned off, it appeared to create a short circuit, which discharged the capacitor between pulses. By switching a constant source and using a switch to pulse the supply, this issue went away. The earth connection with the source is necessary for a frame of reference; otherwise you will get some computational errors.
The resistor, inductor and capacitor are pretty straight forward and are connected in series. These are implemented within the block as:
Resistor:
Inductor:
Capacitor:
The voltage sensors across the resistor and capacitor give those voltages. A current sensor gives the circuit current (which is the same in the resistor, inductor and capacitor). The resistor voltage is multiplied by the current and then integrated over time to get the total energy dissipated within the resistor. I could have added blocks to calculate the energy stored in the capacitor, but for expedience decided to do this calculation manually:
The Results
With the model complete, it was time to run the simulation and check the results. First thing was to set the parameters of the switch trigger so that it was always closed (constant d.c. model). This could let me check that everything was working as it should. I also had the voltage set to 720 V. The following images show the results of the simulation (click for larger versions):
_thumb.png)
Step Voltage Circuit Current & Capacitor Voltage
_thumb.png)
Step Voltage Power Loss Across Resistor
The results show what was expected. The current oscillates due to the inductor/capacitor (I had deliberately selected a slightly under-damped values for R, L and C) The power loss across the resistor was the same as the energy stored in the capacitor (approximately 16330 Joules).
Note: energy stored in the capacitor is 1/2 C V2 = 16,330 Joules
Now it was time to try a pulsed waveform. I worked thorough several scenarios as part of my testing, but for the note I'll just give one. The following images depict the results for a pulse of 0.01 s (100 Hz) period and with the the on/off times being equal:
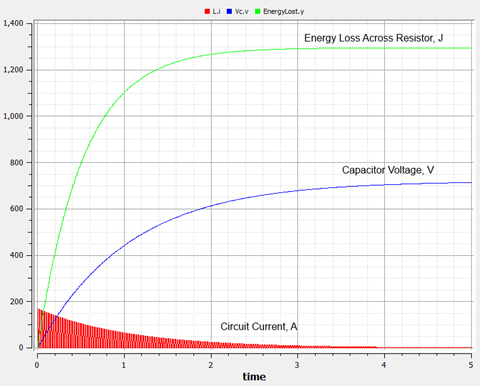
Pulsed Voltage - Resistor Loss, Capacitor Voltage and Circuit Current
As illustrated by the results, the interesting thing is that the energy loss across the resistor is less. In this instance, approximately 1,300 Joules or 8% of the energy stored in the capacitor. This is a massive improvement over losing half the charging energy with a steady d.c. voltage. Obviously, the principal of pulse charging appears to warrant serious investigation in any energy storage application.
Another important conclusion worth noting is that the time to charge does increase significantly. Depending on how any energy storage system is used, this could be important and may warrant particular consideration. It is also worth noting that the magnitude of peak current has been reduced.
Note: the example has been put together primarily as a learning exercise. If this were to be used in a real application, the model would need to be subjected to a more in-depth validation and be made more robust.
Using a Text Based Class
In addition to the process type approach detailed above, OpenModelica has the ability to allow you to enter the problem as a text based Modelica class, which combines the inputs, outputs and maths equations to connect the two together. In some instances, this may be a more productive approach. In addition, the blocks used in the approach above are developed in this manner and by understanding how classes work, you can extend the existing blocks or create your own.
For our RLC problem, the inputs would be the d.c. supply voltage (u(t)) and values for the resistance (R), inductance (L) and capacitance (C). The output is the power loss across the resistor, which is the integral of the instantaneous power (product of resistor voltage and current).
There are several ways to develop the equations connecting the inputs to the outputs. I took the approach of deriving the state space equations by considering Kirchoff's laws and the voltage relations for the energy storage devices (inductor and capacitor). This gave me the following equations:
For a steady input voltage of 720 V, the Modelica class can then be implemented as:
- model RLCCircuit
- parameter Real R = 0.5 "resistance value, Ω";
parameter Real L = 0.02 "inductance value, H";
parameter Real C = 0.063 "capacitance, F";
Real q(start = 0) "charge on capacitor, C";
Real i(start = 0) "current in the circuit, A";
Real u "input voltage, V";
Real vr "voltage across the resistor, V";
Real loss "energy loss across the resistor, J";
- equation
- u=720;
der(q) = i;
der(i) = (1/L)*(u-R*i-q/C);
vr = i*R;
der(loss) = i*vr;
- end RLCCircuit;
Note: 'parameters' indicate fixed (non time varying) variables and 'der' the derivative of a variable. Modelica itself, sorts out what are inputs and output and how they are processed.
On running the simulation, the result is identical to the generated by building the model using the component blocks (see earlier in the note). To use the class with a pulsed input, we would need to modify the equation for u. You could also define other outputs (capacitor voltage, inductor voltage, etc.) if needed.
Wrap Up
Overall I'm pretty impressed. Even with only spending a limited time, to me it is a clean and relatively easy. With a reasonable period of study, it should be quick learning curve to become proficient. As an open source free software tool, OpenModelica, did it's job admirably.
Besides building your own models, for electrical engineering, there are already a lot of predefined base blocks - analogue components, machines, transmission lines and others. If you search around, you will also find additional libraries.
Modelica is not an electrical package in the same way ETAP or DigSilent is, but if you have a particular system you need to analysis, it is well worth considering. It is definitely now on my list of tools.
To give it a try, you just need to visit OpenModelica, download and install the package.