Photovoltaic (PV) - Electrical Calculations 

Photovoltaic (PV) cells (sometimes called solar cells) convert solar energy into electrical energy.  Every year more and more PV systems are installed.  With this growing application, it's a good idea for every practicing professional to have an understanding of the calculations associated with PV cells.

There is a vast amount of PV cells in existence, using numerous materials.  At a very simple level, PV cells function by using solar energy to generate electron-hole pairs, which then separate and flow in the external circuit as current. Examining the physics of this of how the current generation works is not the intent of this note, rather we will look at the electrical calculations surrounding the actual application of real systems.

Electrical Parameters

PV cells are manufactured as modules for use in installations.  Electrically the important parameters for determining the correct installation and performance are:

• Maximum Power - this is the maximum power out put of the PV module (see I-V curve below)
• Open circuit voltage - the output voltage of the PV cell with no load current flowing
• Short circuit current - the current which would flow if the PV sell output was shorted
• Maximum power point voltage - level of voltage on the I-V curve which produces the maximum power
• Maximum power point current - level of current on the I-V curve which produces the maximum power
• Efficiency - measure of the amount of solar energy converted to electrical peak energy

Parameters for PV cells are measured under specified standard test conditions (STC). 

STC is generally taken as 1000 W/m², 25 °C and 1.5 AM (air mass). 

The maximum power output is the peak power which a solar cell can deliver at STC.  While common to rate PV installations based on this value, it is unlikely these power levels will be achieved in practice.

For a list of symbols used, see the end of the note.

Calculation of the output of a system

Nominal rated maximum (kW_p) power out of a solar array of n modules, each with maximum power of Wp at STC  is given by:

     
- peak nominal power, based on 1 kW/m² radiation at STC

The available solar radiation (E_ma) varies depending on the time of the year and weather conditions.  However, based on the average annual radiation for a location and taking into account the efficiency (η) of the cell, we can estimate an average PV system energy yield:

    
- average energy per year produced, kWh

Note: E_ma is given in tables for a particular location and a horizontal plane.

To obtain the anticipated solar radiation requires some research (Internet or local meteorology departments).  If you are using software to perform the calculations, this information is normally provided as part of the program.

The overall efficiency (η) of the solar installation (shading losses, inverter losses, reflection losses, temperature losses, etc.), in a well designed system, these will range from 0.75 to 0.85.

The above calculation is carried out on an annual basis, but could easily be done for any time period (hours, day, month, etc.) by substituting the period mean solar radiation for the annual value. 

For maximum power, any solar radiation should strike the PV panel at 90°.  Depending where on the earths surface, the orientation and inclination to achieve this varies.  Software is normally used for the calculation of this or the use of correction coefficients from the concerned location.

Temperature

As the temperature of PV cells increase, the output drops.  This is taken into account in the overall system efficiency (η), by use of a temperature derating factor η_t and is given by:

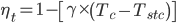
Note: power temperature coefficient (ϒ) is typically 0.005 for  crystalline silicon

Efficiency & Performance

Efficiency: measures the amount of solar energy falling on the PV cell which is converted to electrical energy

Several factors affect the measurement of PV efficiency, including:

• wavelength - PV cells respond differently to differing wave lengths of light, producing varying qualities of electricity
• materials - different PV materials behave differently
• temperature - cells work better at lower temperatures, with efficiency dropping off at higher temperatures
• reflection - any reflected light decreases the efficiency of the cell
• resistance - the cells electrical resistance creates losses, affecting the efficiency

Best Research Cell Efficiencies
Image Source: National Renewable
Energy Laboratory (NREL)

Manufactured PV cells or modules are typically sorted by a binning process into different levels of efficiency.  More efficient cells would have a greater electrical output and hence higher cost.

With the latest development in solar technologies, PV cell are now starting to reach the theoretical maximum limit for semiconductor devices.  The image to the side (click for a larger version) shows the achievable range of efficiencies over differing cell technologies.

In a laboratory, efficiency is measured under standard conditions by the use of I-V curves.  I-V curves are obtained by varying an external resistance from zero (short circuit) to infinity (open circuit).  The illustration shows a typical I-V curve.

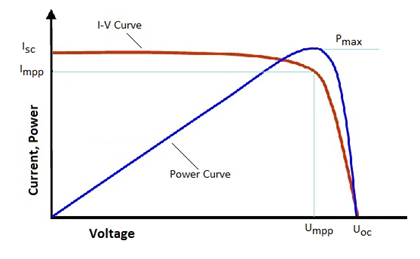
PV Cell, I-V and Power Curves

Power delivered by the PV cell is the product of voltage (V) and current (I).  At both open and closed circuit conditions the power delivered is zero.  At some point in between (around the knee point) the delivered power is a maximum. 

Note: the maximum amount of current that a PV cell can deliver is the short circuit current.  Given the linearity of current in the voltage range from zero to the maximum power voltage, the use of the short circuit current for cable and system dimensioning is reasonable. 

Fill Factor

One way to measure the performance of a solar cell is the fill factor.   This is the ratio of the maximum power to the product of the open circuit voltage and short circuit current:

The higher the fill factor the better.  As a general rule, commercial PV cells will have a fill factor greater than 0.7.  Cells with factors less than this are not really recommended for practical application in larger electricity generation projects.

Maximum Power Point Tracking (MPPT)

A PV module's I-V curve can be generated from the equivalent circuit (see next section).   Integral to the generation of tie I-V curve is the current Ipv, generated by each PV cell.

The cell current is dependant on the amount of light energy (irradiance) falling on the PV cell and the cell's temperature. 

As the irradiance decreases not only is the amount of power reduce, but the peak power point moves to the left. Similarly as the temperature of the cell increases, the power output lowers and the maximum power point again shifts to the left.

With the maximum power point being a variable quantity, dependant on the solar irradiance and cell temperature, modern inverters have mechanisms to track this and always deliver the maximum possible power from a PV cell.  This is called maximum power point tracking (MPPT).

Note: control systems used to carry out MPPT vary the operation around the current operating point to see if the maximum power point has moved.  They then adjust the operating points accordingly.

PV Cell Equivalent Circuit

To understand the performance of PV modules and arrays it is useful to consider the equivalent circuit.  The one shown below is commonly employed.

PV module equivalent circuit

From the equivalent circuit, we have the following basic equations:

- load current in Amperes

- voltage across the shunt branches

- current through the shunt resistor

The current through the diode is given by Shockley's equation:

and

Combining the above equations give the PV cell (module) characteristic equation:

Note: the characteristic equations can be used for find both the output voltage and current. Unfortunately, give that voltage and current appear as they do, there is no analytical solution.  Typically numerical methods would be used to solve the equation.

At the limits, it is easy to use the equation to determine the open circuit voltage and short circuit current.  During open circuit conditions, I=0 and the equation reduces to: 

Typically R_sh is high compared to the open circuit voltage and the last term can be neglected.  Neglecting the term and rearranging the equation gives:

Similarly for the short circuit current, we can set the output voltage to zero, giving:

The assumption that R_sh is much higher than Rs and that I_o is small compared to I.  With these assumptions, the last two terms can be neglected, giving:

The series resistance (Rs), shunt resistance (R_sh) and reverse saturation voltage (I_o) are dependent on the area of the PV cell.  Generally the bigger the cell the larger I_o (bigger diode junction area) and the lower R_s and R_sh will be. 

The characteristic equation can be used to evaluate the effect of various parameters on the performance of the PV cell or module:

• temperature (T) - affects the cell by being part of the exponential term and the value of the reverse saturation voltage.  As the temperature increases, while the exponential will decrease the reverse saturation voltage will increase exponentially. The next effect is to reduce the open circuit voltage of the cell.  Typically the voltage will decrease by 0.35 to 0.5% for each degree increase in temperature.
• series resistance (R_s) - increasing has a similar effect to temperature in that the open circuit voltage will start to drop.  Very high values of Rs will in addition reduced the available short circuit current. 
• shunt resistance (R_sh) - decreasing will provide a greater path for the shunt current, again lowering the cell voltage. 

List of Symbols

See Also

• Photovoltaic (PV) - Utility Power Grid Interface - information on the connection of PV systems to a utility grid and installation advice.