The dc resistance of conductors

This is the first of two posts on the resistance of conductors. In the next post I will look at the ac resistance, including skin effect and show how we can deal with this. To get started, this post will look at the simpler case of dc resistance and how it can be calculated.
DC Resistance to IEC 60287
The international standard for conductors is IEC 60287. The standard classifies conductors according to four classes:
- Class 1: solid conductors
- Class 2: stranded conductors
- Class 5: flexible conductors
- Class 6: flexible conductors (more flexible than class 5)
For each class of conductor, the standard defines the maximum allowable resistance at 20 oC:
| Minimum Resistance of Conductors in mΩ/m |
| CSA mm² | Copper (plain) | Copper (tinned) | Aluminium |
| class 1 & 2 | class 5 & 6 | class 5 & 6 | class 1 & 2 |
| 0.5 | 36.0 | 39.0 | 40.1 | - |
| 0.75 | 24.5 | 26.0 | 26.7 | - |
| 1 | 18.1 | 19.5 | 20.0 | - |
| 1.5 | 12.1 | 13.3 | 13.7 | - |
| 2.5 | 7.41 | 7.98 | 8.21 | - |
| 4 | 4.61 | 4.95 | 5.09 | - |
| 6 | 3.08 | 3.30 | 3.39 | - |
| 10 | 1.83 | 1.91 | 1.95 | 3.08 |
| 16 | 1.15 | 1.21 | 1.24 | 1.91 |
| 25 | 0.272 | 0.78 | 0.795 | 1.20 |
| 35 | 0.524 | 0.554 | 0.565 | 0.868 |
| 50 | 0.387 | 0.386 | 0.393 | 0.641 |
| 70 | 0.268 | 0.272 | 0.277 | 0.443 |
| 95 | 0.193 | 0.206 | 0.210 | 0.320 |
| 120 | 0.153 | 0.161 | 0.164 | 0.253 |
| 150 | 0.124 | 0.129 | 0.132 | 0.206 |
| 185 | 0.0991 | 0.106 | 0.108 | 0.164 |
| 240 | 0.0754 | 0.0801 | 0.0817 | 0.125 |
| 300 | 0.0601 | 0.0641 | 0.0654 | 0.100 |
| 400 | 0.0470 | 0.0486 | 0.0495 | 0.0778 |
| 500 | 0.0366 | 0.0384 | 0.0391 | 0.0605 |
| 630 | 0.0283 | 0.0287 | 0.0292 | 0.0469 |
| 800 | - | - | - | 0.0367 |
| 1000 | - | - | - | 0.0291 |
| 1200 | - | - | - | 0.0247 |
DC Resistance - calculation
For solid conductors the resistance (theoretically) can also be calculated using the standard formula:
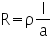
If the length (l) is in metres, cross sectional area, a in m2 (mm2 x10-6) and resistivity ρ in Ω-m, then the Resistance will be in ohms. The resistivity in Ω-m (at 20 oC) for copper is 1.72x10-8 and for aluminium 2.82x10-8.
The above formulae does not take into account manufacturing tolerances, compactness of stranded conductors, etc. These will result in the calculated resistance differing from any actual measured resistance. For general use it is probably better to use the figures from the IEC 60287 table, rather than calculation using the above formula.
Temperature dependence
The above values of resistance are based on a temperature of 20 oC. Resistivity of the conductor will varies with temperature, with the resistance increasing as temperature increases. This variation can be simplified to a linear function for a reasonable temperature range as follows:
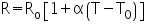
- R = the resistance of the conductor at temperature T
- R20 = conductor resistance at 20 oC
- T = operating temperature of the conductor
- α = temperature coefficient of resistivity
Actual values of α, depend on the composition of the material in addition to the temperature. For both copper and aluminium, α taken as 0.0039 will give sufficient accuracy for most conductor calculations.
The ac resistance of conductors ->