Back to Basics - Ohm’s Law
The Basics

Georg Ohm Electrical engineering has a multitude of laws and theorems. It is fair to say the Ohm's Law is one of the more widely known; if not the most known. Developed in 1827 by Georg Ohm the law defines the relationship between voltage, current and resistance in an electric circuit.
Voltage is the force that is used to drive current around an electric circuit. This can be provided by batteries, generators, etc., is measured in Volts (V) and denoted by the symbol V. The voltage drives electric current around the circuit and this current does the useful work (heating an element in a light bulb for example). Electric current is typically described as the flow of electrons around a circuit, is measured in Amperes (A) and denoted by the symbol I. Resistance is the opposition an electric circuit provides to the flow of current; it limits the amount of current flowing when a voltage is applied. Resistance is measured in Ohms (Ω) and denoted by the symbol R.
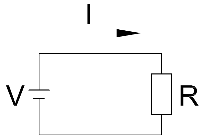
The illustration shows a simple circuit consisting of a supply voltage V and resistance R around which flows a current I. Ohm's law provides the relationship between these quantities:
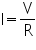
That’s it - really straight forward and simple. In words we can say the relationship between voltage and current in a circuit is a constant - the resistance.
The law can of course to be rearranged to give each parameter:
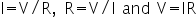
A little more complexity
The above is strictly true for direct current (dc) circuits. In a dc circuit the current flows in one direction (positive to negative) and is a constant value. This changes in alternating current (ac) circuits - see the note article on Alternating Current Theory. Because the current is constantly changing in an ac circuit, the magnetic fields are in motion and introduce additional constraints on the flow of current. In addition to resistance we have a new parameter called reactance. These combine into a quantity called impedance which opposes the flow of electric current when a voltage is applied.
Like resistance the ac impedance is measured in Ohms (Ω) and is denoted by the symbol Z. The good news is that impedance behaves like resistance and Ohm's Law still applies:
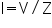
Note: when talking about dc circuits the quantities (V, I and R) are scalar values. In ac circuits these are vector quantities and the mathematics can be more complicated.
Even more complexity
To fully round off the discussion on Ohm's Law, it should be noted that it can be reformulated to apply in a more general sense to many physics problems, other than it’s pure application to dc or ac circuits. This reformulation was carried out by Gustav Kirchhoff and is:
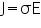
In this representation J is the current density at some location (in a material or free space) and is measured in Ampere per metre squared. E is the electric field in Volts per metre and 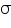 is the conductivity of the material in Siemens per meter. Conductivity is the inverse of resistivity (Ohm meter).
is the conductivity of the material in Siemens per meter. Conductivity is the inverse of resistivity (Ohm meter).
There are other representations of Ohm's Law, but these are starting to transgress into the realm of theoretical interest only. If you are interested in an application of the above formulae, you can look at the Earth Electrode Resistance note.
Being such an important and fundamental electrical law, most of us have had the experience learning and applying Ohm’s law. If you have any tips or other Ohm’s law goodies to share, please add these below.
See Also