Three Phase Current - Simple Calculation

By Steven McFadyen on March 1st, 2009

The calculation of current in a three phase system has been brought up on our site feedback and is a discussion I seem to get involved in every now and again. While some colleagues prefer to remember formulas or factors, I prefer to resolve the problem step by step using basic principles. I thought it would be good to write how I do these calculations. Hopefully it may prove useful to someone else.

Three Phase Power and Current

The power taken by a circuit (single or three phase) is measured in watts W (or kW). The product of the voltage and current is the apparent power and measured in VA (or kVA) . The relationship between kVA and kW is the power factor (pf):

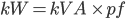
which can also be expressed as:

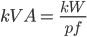
Single phase system - this is the easiest to deal with. Given the kW and power factor the kVA can be easily worked out. The current is simply the kVA divided by the voltage. As an example, consider a load consuming 23 kW of power at 230 V and a power factor of 0.86:

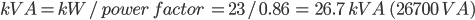
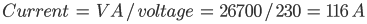
Note: you can do these equations in either VA, V and A or kVA, kV and kA depending on the magnitude of the parameters you are dealing with. To convert from VA to kVA just divide by 1000.

Three phase system - The main difference between a three phase system and a single phase system is the voltage. In a three phase system we have the line to line voltage (V_LL) and the phase voltage (V_LN), related by:

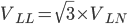
or alternatively as:

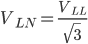
to better understand this or gain more insight, you can read the Introduction to Three Phase Electric Power post

To me the easiest way to solve three phase problems is to convert them to a single phase problem. Take a three phase motor (with three windings, each identical) consuming a given kW. The kW per winding (single phase) has to be the total divided by 3. Similarly a transformer (with three windings, each identical) supplying a given kVA will have each winding supplying a third of the total power. To convert a three phase problem to a single phase problem take the total kW (or kVA) and divide by three.

As an example, consider a balanced three phase load consuming 36 kW at a power factor of 0.86 and line to line voltage of 400 V (V_LL) :

the line to neutral (phase) voltage V_LN = 400/√3 = 230 V
three phase power is 36 kW, single phase power = 36/3 = 12 kW
now simply follow the above single phase method

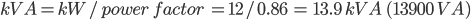
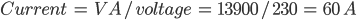
Easy enough. To find the power given current, multiply by the voltage and then the power factor to convert to W. For a three phase system multiply by three to get the total power.

Personal note on the method

As a rule I remember the method (not formulae) and rework it every time I do the calculation. When I try to remember formulae I always forget them soon or become unsure if I am remembering them correctly. My advice would be to always try remember the method and not simply memorize formula. Of course if you do have some super ability at remembering formula, you can always keep to this approach.

Using Formulas

Derivation of Formula - Example

Balanced three phase system with total power P (W), power factor pf and line to line voltage V_LL

Convert to single phase problem:
$P_{1 p h} = \frac{P}{3}$

Single phase apparent power S_1ph (VA):
$S_{1 p h} = \frac{P_{1 p h}}{p f} = \frac{P}{3 \times p f}$

Phase current I (A) is the single phase apparent power divided by the phase to neutral voltage (and given V_LN=V_LL / √3):
$I = \frac{S_{1 p h}}{V_{L N}} = \frac{P}{3 \times p f} \frac{\sqrt{3}}{V_{L L}}$

Simplifying (and with 3 = √3 x √3):
$I = \frac{P}{\sqrt{3} \times p f \times V_{L L}}$

The above method relies on remembering a few simple principals and manipulating the problem to give the answer.

More traditionally formulas may be used to give the same result. These can be easily derived from the above, giving for example:

$I = \frac{W}{\sqrt{3} \times p f \times V_{L L}}, i n A$

Unbalanced Three Phase Systems

The above deals with balanced three phase systems. That is the current in each phase is the same and each phase delivers or consumes the same amount of power. This is typical of power transmission systems, electrical motors and similar types of equipment.

Often where single phase loads are involved, residential and commercial premises for example, the system can be unbalanced with each phase have a different current and delivering or consuming a differing amount of power.

Balanced Voltages

Luckily in practice voltages tend to be fixed or very by only small amounts. In this situation and with a little thought it is possible to extend the above type of calculation to unbalanced current three phase systems. The key to doing this is that the sum of power in each phase is equal to the total power of the system.

For example, take a 400 V (V_LL) three phase system with the following loads: phase 1 = 80 A, phase 2 = 70 A, phase 3 = 82 A

the line to neutral (phase) voltage V_LN = 400/√3 = 230 V
phase 1 apparent power = 80 x 230 = 18,400 VA = 18.4 kVA
phase 2 apparent power = 70 x 230 = 16,100 VA = 16.1 kVA
phase 3 apparent power = 82 x 230 = 18,860 VA = 18.86 kVA
Total three phase power = 18.4 + 16.1 + 18.86 = 53.36 kVA

Similarly given the power in each phase you could easily find the phase currents. If you also know the power factor you can convert between kVA and kW as shown earlier.

Unbalanced Voltages

If the voltages become unbalanced or there are other considerations (i.e. unbalanced phase shift), then it is necessary to revert to more traditional network analysis. System voltages and currents can be found by drawing out the circuit in full detail and using Kirchhoff's laws and other network theorems.

Network analysis is not the intent of this note. If you interested in an introduction you can view our post: Network Theory – Introduction and Review

Efficiency & Reactive Power

Other things to consider while carrying out calculations may include the efficiency of equipment. Knowing that efficiency of power consuming equipment is the output power divided by the input power, again this can easily accounted.for Reactive power is not discussed in the article and more details can be found in other notes (just use the site search).

Summary

By remembering that a three phase power (kW or kVA) is simply three times the single phase power, any three phase problem can be simplified. Divide kW by the power factor to get the kVA. VA is simply the current times the voltage, so knowing this and the voltage can give the current. When calculating the current use the phase voltage which is related to the line voltage by the square root of three. Using these rules it is possible to work out any three phase problem without the need to remember and/or resort to formulas.

Theory, Fundamentals, Three Phase, Calculations, Power, Voltage, Theory

More interesting Notes:

Possibly related posts:

Steven McFadyen

Steven has over twenty five years experience working on some of the largest construction projects. He has a deep technical understanding of electrical engineering and is keen to share this knowledge. About the author

myElectrical Engineering

comments powered by Disqus

View 60 Comments (old system)

Faiz Ahmad says:

9/1/2011 2:11 PM

Hi All, This is wrong calaculation. Please check it .if u divide kw by p.f u will get kVA not KW. three phase power is 36 kW, single phase power = 36/3 = 12 kW now follow the above single phase method kVA = kW / power factor = 12/0.86 = 13.9 kW (13900 W) Current = W / voltage = 13900/230 = 60 A
- Steven says:
  
  9/1/2011 2:11 PM
  
  Thanks for pointing out the mistake. I have now changed it to show kVA.
Shahbaz Ahmed says:

9/1/2011 2:11 PM

If I have a system having Amperes on each phase as 80A, 70A, 82A and VLL is 400V and VLN is 210 V. Kindly share how to calculate its power consumption in KVA
- Steven says:
  
  9/1/2011 2:11 PM
  
  For each phase the VA is current x voltage (i.e. 80x210 = 1680 VA). Add up the three phases = 48720 VA (or 48.72 kVA). Alternatively add the currents and multiply by the voltage (80+70+82)*210 = 48.72 kVA. By the way, I think you probably wanted to say 230 V (not 210 V) if VLL is 400 V.
Ravinder Mehta says:

9/1/2011 2:11 PM

How to get power factor three phase motor specification as below

Watt - 110

Current - 0.80

RPM - 1350

If any body knows how, please can you teach me...
- Steven says:
  
  9/1/2011 2:11 PM
  
  The rpm does not affect it. Also depends on if it is three phase or single phase and the voltage. Motor rated power is normally the output power, so to be fully accurate you need to consider the efficiency. Ignoring efficiency and assuming single phase 230 V, the VA would be 184 (230 V x 0.8 A) and power factor 110/184 = 0.6.
zubah Kortimai says:

9/1/2011 2:11 PM

Please can some body teach me, what is the current across each line of a 167 kVA 3 phase generator with a line voltage of 240 volt
- Steven says:
  
  9/1/2011 2:11 PM
  
  It is a three phase generator, each phase supplies 167/3 = 56 kVA. Assuming delta connected, the line voltage is across each phase and the current is 56,000/240 = 230 A. If it is star connected than the phase voltage is 240/sqrt(3) = 138 V and the current is 56,000/138 = 400 A. The three phase calculator may also help you: http://myelectrical.com/tools/3phasecalculations.aspx
TC says:

9/1/2011 2:11 PM

I have a small 400 V three phase 4 wire (star) installation with the following resistive loads on each;
- red 30kw
- white 20kw
- blue 10kw
I need to calculate the line current in each of the three phases can some one please help with a formula?
- Steven says:
  
  9/1/2011 2:11 PM
  
  I would treat these as three separate single phase problems. The phase voltage is 400/ √(3) = 230 V. To convert kW to kVA you need the power factor (you could just use kW, but you would have some error). For the red phase, assuming a power factor of 0.95, the kVA is 20 kW / 0.95 = 21 kVA. The line current is then the kVA divided by the voltage, i.e. 21,000 / 230 = 91 A. Similar method for the other phases.
John says:

9/1/2011 2:11 PM

I am calculating the current in a 3 phase 380 V balanced Y system with a single motor load of 746 watts with a power factor of 0.72 and am getting different results when using the approaches suggested above.

746/3 = 249 watts per phase
249/0.72 = 345 VA per phase
V Line-Line = 380 V
380/1.73 = 219 V Line-Neutral (Phase Voltage)
345/219 = 1.57 A per Phase = Line

But a different result when using
I = kW / ( √3 x pf x VLL ), in kA
I = 249/(1.73*0.72*380) = 0.52 A

Any ideas where I'm going wrong?

Also, if this was a Delta configuration, then the line current would be
345/380 = 0.90 I Phase
I line = 0.90 * 1.73 = 1.57 A
Which brings up another question. Why is the Y and Delta line current the same? I thought Y systems had lower line currents and that was one advantage to using them. Any help greatly appreciated!
- Steven says:
  
  9/1/2011 2:11 PM
  
  The kW in your formula is the three phase kW, so I think you should be using 746 (not 249).
  
  I'm not sure if this helpful, but I will derive the formulae using the above method so you can see the two tie together.
  
  Power (3-phase) = kW, therefore per phase = kW/3
  kVA per phase = kW per phase / power factor
  = kW / (3 x pf)
  
  Phase Voltage = VLL/√3
  Current I = kVA per phase / phase voltage
  
  = kW / (3 x pf) divided by (VLL/√3)
  = (kW x √3) / (3 x pf x VLL)
  = kW / (√3 x pf x VLL) - your formulae
  
  I've always been bad a remembering formulae, so I prefer to remember concepts/methods. To me it is easier, and if necessary I can always derive the formulae. If remembering is formulae more easy, just go with that.
  
  On the Star Delta. Consider the motor as a black box taking some power. Power is related to the voltage and current so regardless of star or delta if the box taking the same power, both voltage and current will be the same. What normally happens in star is that because the voltage is less across each winding, you end up delivering less power then you would in delta (less power is less current).
  
  I do have my 'Motor Starting - Star Delta' post drafted which explains this in more detail. I'm just holding off on posting as the upgrading of site is going really well. The new posting/commenting system is way better than the current one and I'm now just waiting to use it. Planning to make the new site live in about a week.
  - John says:
    
    9/1/2011 2:11 PM
    
    Thanks Steven! That definitely clarifies the error in my calcs.
    
    As a practical matter when literature specifies "line" voltage does this correspond to the country standard; ie 480 VAC 3 phase industrial power in the US?
  - Steven says:
    
    9/1/2011 2:11 PM
    
    John, line voltage is dependant on country (and varies within countries). If you do a site search for "International Voltages" we have a Wiki page which lists some of these (may be slightly out of date). Robert, I make the line current as 33.6 A. You can't divide the current by three (power kW or kVA - yes). If you think of a motor, each winding identical then they would each consume a third of the power. The current just does not work that way.
Robert Shenuda says:

9/1/2011 2:11 PM

Hi all,

Kindly I want to know in 3 phase distribution ( example a house)

Say I have 29 kVA ... equals to 36,250watts (PF=0.8)

kVA =1.73*E*I/1000 ... given E=230 Vac

So (I) would be equal to 72.79A ... is this 72.79 divided by the 3 phase, i.e does each phase has a load of 24.26 A ?

I hope to get some answers and if any reference on web would be great. thanks :)
fawbish says:

5/28/2012 3:21 PM

Hi,

I believe your equation

I = kW / ( √3 x pf x VLL ), in kA

Should VLL not be VLN here?

I just went through and got a few strange results, and realised that earlier you state

VLL = √3 x VLN

Hence I wondered why you would then multiply VLL again by √3.

Is this wrong?

Cheers,

Nathan
- Steven says:
  
  5/30/2012 4:57 PM
  
  I pretty sure the formula given is correct. Within the body of the post I have added an example of how to derive the formulae. Please check this and if you find any errors or mistakes let me know.
Binesh says:

6/12/2012 9:16 AM

I have 3 loads on each phase as

L1-2=19.74 VA,
L2-3=16.91 VA
L1-3=13.81 VA

Please tell the capacity of the transformer required. How to use the formula and which formula to find it out..???
- Steven says:
  
  6/13/2012 1:25 PM
  
  As a general guide I would just add up the VA, use a 70% load factor. Total VA = 50.46, using 70% require 72 VA transformer (chose next standard size up).
  You need to be cognisant of what you are supplying and if this will affect the sizing (for example if the load is non-linear).
panuci says:

6/21/2012 7:28 AM

3 phase system, if 1 phase out ( fuse cut0ff burn ) for meter kwh, can make the electricity bill increase..??
- Steven says:
  
  6/21/2012 11:05 AM
  
  Not directly related to the post, but this is a great question. Would it be possible for you to ask this in our question section. I think you will get a better response and help our other users. I will also put together a proper answer when I get some time.
tukang says:

6/23/2012 10:48 AM

I have electric motor from USA, 3 phase 230 Volt 60 Hz. Can we use in Asia (380 volt 50 Hz)? or need modification on the motor.
thank you very much
- Steven says:
  
  6/24/2012 6:27 AM
  
  I would say you cannot use the motor at 50Hz, 380V. The motor would be running faster due to the frequency. In addition the voltage would be increase the torque and current for which the motor is likely not designed.
- jimmy77 says:
  
  7/10/2013 8:48 AM
  
  I have the same issue with our Contractor supplying pump motor 50hz, where-in our system here is 60 hz.
  To make the situation confusing, the contractor got the confirmation from the manufacturere. ABB that according to their calculation, that 50hz motor would be fine for 60hz system.
  
  Need your excellent advise Mr. Steven.
  
  Thank you so much!
Pip says:

7/22/2012 3:27 AM

I deal with unbalanced systems on a frequent basis and am trying to figure out how to calculate the amps drawn on each leg. For example my current system has the following power draw:
A-B 56,000 Watts
B-C 23,000 Watts
A-C 17,000 Watts

It's hooked to a 3 phase wye system 208/120.

Thanks.
- Steven says:
  
  7/25/2012 2:44 PM
  
  Pip, sorry for the delay – busy relocating countries/jobs at the moment.
  
  With A-B, B-C and A-C you are looking a loads in a delta connected system. 208/120 is the voltage for a delta (208) / star (120), connected system. You would have 208 volts across each of the loads you gave and can find the current using Ohm’s law (i.e. A-B 56,000/208 = 269 A in that branch).
  
  Strictly speaking you should be using kVA (which you can obtain by dividing the watts by the power factor).
  
  Also make sure you are really dealing with a delta system and not a star-connected system (i.e. A-N, B-N and C-N).
- Pip says:
  
  7/25/2012 6:31 PM
  
  Steven, let me give you a few more details.
  
  I work in the entertainment industry and definitely work with a star connected (wye) system where all legs measured to neutral is 120V and leg to leg is 208V. What I need to know is how many amps I'm pulling on each individual leg. We have a lot of loads that are connected line-neutral and figuring out those loads is easy. Where I have issues is when we have loads connected across two phases. If the system is perfectly balanced I again have no issues figuring out the amps drawn on each leg. But in the example I gave you the loads are quite obviously not balanced. Now the calculation you gave me gives me the total amps on A-B but it doesn't tell me how many amps I'm pulling on A and how many amps I'm pulling on B. I know when you are dealing with loads connected across phases figuring out the current isn't as straight forward as using ohms law. I just don't know how to go about it.
- Steven says:
  
  7/27/2012 11:19 AM
  
  I understand a little more now (perhaps not fully). I think you can still convert to three single phase problems, with phase A having halt of the AB load and half of the AC load. Similarly for phase B (1/2AB + 1/2BC) and phase C (1/2BC + 1/2AC).
  
  Phase A - 1/2 56,000 + 1/2 17,00 = 36,500 W
  - divide by 120 V gives 304 A in the line conductor
  
  - similar for the other phases, giving B=329 A and C=167 A
  
  I have assumed the power factor =1 and W = VA.
BPE says:

9/27/2012 9:31 PM

Thanks for the write up. In your example where you break down a 3-phase problem to a single phase problem with the 36kW load, you get 60A. That 60A is total rms current for a single phase, not the peak current, correct? So is it as simple as multiply by 3 to get the total, 3-phase rms current?
- Steven says:
  
  9/28/2012 11:28 AM
  
  Your correct it is the RMS current. You could do the calculation in terms of peak current if you wanted (for a sine wave the relationship between the peak and RMS is the square root of two).
  
  You do not need to multiply by 3. The current calculated is the line current - if you place an ammeter in the circuit, this is what you will measure.
- BPE says:
  
  9/28/2012 5:35 PM
  
  So it is the second part of your reply that I don't understand. In a three phase system, the amount of current going through one of the phases is not a fraction of the amount of current going through all three? If I was to create a 3 phase fault by shorting all three phases together, how much current would go through the fault towards the load?
  
  Also, thanks again for posting and all of your help
- Steven says:
  
  9/29/2012 9:36 AM
  
  Try to look at the following post. In the post, the motor is a three phase load, where as the socket is single phase - in each case case you have the line current which is common (for example, the current flowing in L1).
  
  http://myelectrical.com/notes/entryid/172/three-phase-power-simplified
  
  After looking at the above post, please let me know if it makes more sense or if you still need a better explanation.
  
  If you create a fault the current will increase (you have reduced the circuit impedance with the fault). Current won't flow through the fault to the load (or very little will). At the fault location, because the phases are shorted, they will be at nearly the same voltage (close to zero depending on the impedance). The load sees this voltage and no current will flow.
  
  Hope this makes sense.
alo says:

10/10/2012 8:54 PM

How can I calculate power factor(pf) if I know the kW, V, Hz and reactive power?
For a three phase AC generator.
Thanks
- Steven says:
  
  10/11/2012 2:48 PM
  
  Once you know the kVA, you can calculate the power factor form pf=kW/kVA.
  
  To find the kVA you can use sqrt(kW^2 + kWr^2), where kWr is the reactive power.
- tian says:
  
  12/7/2012 6:09 AM
  
  is it possible to find the power factor given the reactive power(VAR) and real power(KW) by this equation? tanθ=Q/P
dilan says:

11/16/2012 5:59 AM

Hi all, i have problem in total current computation from ;three phase and single phase, the system is 380v 3-phase, line to neutral is 220.
i computed the current from line to neutral AN=80.6, BN= 65.8, CN=73.2a
three phase current is 491.5a.

my question is do i need to multiply 80.6a to 1.732 to convert in 3 phase?
kindly correct my computation:

I=1.732(80.6)+491.5A
I=631.09
- Steven says:
  
  11/16/2012 9:43 AM
  
  The three phase current as you are trying to calculate it does not exist. In the A phase you have 80.6A, B phase 65.8A and C phase 73.2A - that's it. You still have your three phase system, with the current in each line being slightly different (if all the line currents were the same it would just be a balanced three system).
  
  Because you have an unbalanced system, you will have some current in the neural line. You can calculated this be summing the A, B and C phases, taking into account the phase difference (easiest to do this using complex notation).
  
  Three phase simply means you have three windings instead of one; giving you the A, B and C phases (and if star connected a neutral conductor). In a single phase system you would only have one winding, giving you a single phase (live and neutral).
  
  Hope this makes some sense.
- dilan says:
  
  11/16/2012 11:10 AM
  
  thank you very much for the reply, but how to calculate the total ampere of the system, if A phase 80.6A, B phase 65.8A, C phase 73.2A. and total current of 491.5A from the three phase motors. should i combine/sum phase A, phase B, Phase C and 491.5A. to get the total current. so that i can assign suitable cable and breaker?
  
  thanks..
- Steven says:
  
  11/16/2012 6:04 PM
  
  You don't need to combine the current - just take the worse case line current for sizing cables/breakers.
  
  You give the worse case as 80.6A. I'm not sure of where you are getting your 491.5A from. If the 491.5A is an existing or additional loads to the 80.6A, you would need to add to get the total current (i.e. 572.1A).
  
  To avoid any misunderstanding, the following post may also help you:
  
  http://myelectrical.com/notes/entryid/172/three-phase-power-simplified
- dilan says:
  
  11/16/2012 11:52 PM
  
  491.5A is a total current of three phase motor using traditional method of current calculation.
  
  one more question. can i connect single phase motors to line-neutral?like air compressor & pump motor?
  
  thanks.
- Steven says:
  
  11/17/2012 10:25 AM
  
  I don't see any problem in connecting the single phase motor to line/neutral. This is done all the time (fridge or toilet extract fan in your house for example). Just try to balance your single phase loads as much as possible across all three phases.
- dylan dre says:
  
  11/18/2012 2:32 AM
  
  Thank you very much Steven..
dilan says:

11/26/2012 3:04 AM

Hi Steven, how to get the total KVA of the system if Line AB =642.24amp. BC=651.85A, AC=651.84A, supply voltage 220 line to line. Power factor 0.86, and what size of breaker and cable should I use. Kindly show the computation. Thanks.
- Steven says:
  
  11/26/2012 6:11 AM
  
  dilan,
  
  the kVA would be ( 642.24 + 651.85 + 651.84) * 220
  = 428102 VA = 428.1 kVA
  the kW would be 428.1 x 0.86 = 368.2 kW
  
  For the breaker, I would likely be looking at 800 A (posibly something like a MasterPact NT or NW, depending on other parameters) and setting the overload protection in the range of 710 A (this is plus 10%).
  
  For the cable size I'll refer you to our calculator as it depends very much on the type of cable and installation:
  http://myelectrical.com/tools/cable-sizing-calculator
  
  After looking at the cable size calculator, if you have any questions on using it (or questions on the breaker selection), you can ask in the questions section of the site:
tian says:

12/3/2012 2:20 AM

hi,i would like to ask if getting the current in any configuration (delta or star) is it always the power in kva to be used?.i always had some trouble in this.pls help
- Steven says:
  
  12/3/2012 3:59 AM
  
  tian,
  
  There is always more than one way to do things. I like to use kVA as this is just the voltage multiplied by the current. If you know the kVA and voltage, it is very easy to work out the current. If you wanted to do all your calculations in kW, you could - but you would need to include the power factor as well in any calculation.
tian says:

12/7/2012 5:47 AM

Thanks Steven, it helps a lot. But if you don't mind, I would like to ask a few more question about the apparent power and complex power. What is the difference between the two. I have a book here about circuits it tells that the key to solving problems about three phase is to find the current. I know that it is right but how can i used it to find the value of complex power?? And the value of the impedance and the reactance if required.
- Steven says:
  
  12/10/2012 7:45 AM
  
  I guess in a simple way, complex power is understanding the the real and reactive components are 90° out of phase. The following note touches briefly on the topic of complex power:
  
  alternating-current-circuits
  
  Have a read of the note and if you are still unclear, you can add a comment to post.
Daria says:

12/19/2012 2:39 PM

Dear Steven -

I am a student and I've been struggling to understand something: if we have a balanced STAR connection with a certain apparent power consumption (VA), will this power change if we switch the connection to DELTA?

I know this probably is easy to understand, but I got myself to a completely confused state. Thank you!
- Steven says:
  
  1/13/2013 6:41 AM
  
  In general when connecting in delta you have a higher voltage on each leg, so I would say you consume more power. I try not to think like that as it confuses me as well and there is sometimes more to it than that. My advice would be to look at your actual situation and analysis it to see the effect of changing from star to delta. Also be aware that if draw more power, you equipment may not have been designed for it.
shyam says:

12/21/2012 11:55 AM

Sir, when a voltage dip occurs current increases, so instead of dimming, a bulb should glow brighter but the reverse thing happens, why?
- Steven says:
  
  1/13/2013 6:48 AM
  
  I believe that as you lower the voltage across the lamp, the current would reduce and the brightness (think of the lamp as a resistance).
Francois says:

5/21/2013 2:39 PM

Hi Steven, I drive a centrifugal water pump with a three phase motor. I measure the Power (kW) required by the electrical motor. If the voltage supplied from the grid changes within acceptable tolerances, say 5%, what would you expect will happen to the Power (kW) which I measure?. I expect it to stay the same. Am I correct?
Sunil Agarwal says:

5/22/2013 3:59 PM

Hi Steven,
Thanks for sharing your knowledge, it really helped me understanding the theory. And now I would like to know how does the calculation works when a generator has to be used? For Example :-
Each phase of 3 phase machine takes a load of 16 amps, So how do I calculate how many KVA generator is required ? Does Power Factors plays any role?
- Steven says:
  
  5/23/2013 8:32 AM
  
  It works the same a for a consumer of power. Just multiply the current by the phase-neutral voltage (to get the power per phase) and then by 3. The power factor only comes into play if you want to see the kW (just multiply the kVA by the power factor).
Abdulla says:

5/30/2013 7:45 AM

Hi steven sir,

I want to know in motors we use capacitor, we use star connection for starting 3 phase, is it because the current lags the voltage by 90 degree in an coil or is it for a different reason..

Regards
Abdulla
Confused says:

6/15/2013 6:49 PM

Sorry if this is a simple question. What is the difference between three phase power factor and single phase power factor.
Thanks.
- Steven says:
  
  6/16/2013 8:48 AM
  
  The power factor is the ratio of the real work to the apparent power. The same definition holds for both three phase and single phase systems.
  
  You can find more information on power factor here:
  http://myelectrical.com/notes/entryid/197/power-factor
  
  As a note, it is possible to have a different power factor in each phase of a three phase system. Generally when people talk about power factor, they are concerned with the overall system. If you are looking at it on a phase by phase you may need to be a little careful.
jcdelao says:

6/28/2013 8:28 PM

Hello everybody,

I would appreciate if you can help me with this problem I have:

What is the current of an 647kW, 577V three-phase load with cosFI=0.91?

Thank you
- Hareesh says:
  
  6/29/2013 7:45 AM
  
  Dear jcdelao,
  
  Using the formula, [Sqrt3 x V x I x Cos (Phi)= Power (Watts)] , the current comes to be about 711 A.
  
  Assuming 577 V is Line Voltage and load is balanced.

Comments are closed for this post:

have a question or need help, please use our Questions Section
spotted an error or have additional info that you think should be in this post, feel free to Contact Us